Inverse Matrix aus Minimalpolynom

M(A) sei Minimalpolynom von A (invertierbar). M(A) = M(lamda(k)) = 0, lamda(k): Eigenwert von A;  M(0) ungleich 0, da A invertierbar.
Multipliziert man M(A) mit einem Faktor welcher bewirkt, daß M' (0) = -1 und verschiebt dieses Polynom so, dass es duch den Nullpunkt geht:

M'(x) = - M(x) / M(0); P(x) = M'(x) + 1

dann ist P(0) = 0 und P(lamda(k)) = 1.    P(x) = ax + bx² + cx³..... Nun braucht man nur mehr durch x dividieren.

P'(x) = P(x) / x

Das Polynom hat nun den Grad(P') = Grad(M) - 1

P'(lamda(k)) = 1 / lamda(k); P'(A) = Inverse (A)

Zusammengefasst:

P'(A) = ( 1 - M(x) / M(0) ) / x

Beispiel : Die Matrix 3 hat das Polynom x - 3
P'(A) = ( 1 - ( x - 3 ) / - 3 ) / x = ( 1 + x / 3 - 3 / 3 ) / x = x / 3x = 1 / 3
Für diagonalähnliche Matrizen leicht nachvollziehbar: Für AT = TD steht nun in der Diagonale statt lamda(k) :   1 / lamda(k) = P'(lamda(k))
Anwendungen:
Diagonalähnliche Matrizen mit Eigenwerten 1 und -1 - ausschließlich - , sind sich selbst invers, wenn sie symmetrisch sind, sind sie orthogonal. Das kann man auch anders leicht beweisen. Mit diesem Verfahren sieht man aber sofort:
Die Umkehrung gilt auch. Beispiel: Die punktsymmetrischen Lorentz-Transformationen:*


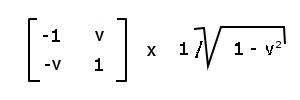
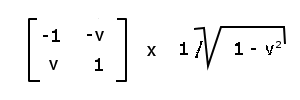
Andere Anwendungen:
Alle Matrizen mit dem Minimalpolynom xⁿ-1 (Einheitswurzeln) sind zu A^n-1 invers.
Das Gleichungssystem A x = b hat die Lösung x = v - A^-1 * y mit y = A v - b (v->x : y->0). Nimmt man für A^-1 "Q(A)", eine Näherung von P'(A) und x _k = x _{k - 1} - Q(A) * y _{k - 1}, so erhält man eine allgemeinere Richardson - Iteration.

Das Minimalpolynom der inversen Matrix:
Mit dem Minimalpolynom einer invertierbaren Matrix P(A)= a₀* x ⁰ +....a_k* x ^k,
hat man auch das Minimalpolynom der Inversen P(A^-1)= (a₀* x ^k +....a_k* x ⁰)/a₀.
Beweis:
Setzt man A^-1 in das neue Polynom ein, und multiplizert es dann mit A ^k so hat man wieder das originale Minimalpolynom in A (Faktor a₀ unberücksichtigt). Da aber A ^k nicht null ist, muss der andere Faktor des Produkts null sein. Das neue Polynom ist also ein Nullpolynom in A^-1. Aber ist es auch minimal?
Angenommen es gibt ein kleineres minimales Polynom für A^-1. Vertauscht man die Rollen von A und A^-1, ergäbe das ein kleineres Polynom für A im Widerspruch zur Voraussetzung P(A) ist minimal. Also k ist der kleinste Exponent mit P(A)=0.

Ludwig Resch

* Hier wird die Koordinatenachse mitgenommen.