Wo ist Unendlich?

Jeder kennt die spitz zulaufenden Papiertüten in der man Kirschen kaufen kann.
In der "Theorie der Isentropen Welt". werden unendlich viele Tennisbälle erwähnt, die man nicht zerstören kann, wenn man nicht allmächtig ist, d.h. man wäre fähig alle Tennisbälle auf einmal zu zerstören. Wo könnte man so viele Tennisbälle in unserer Welt unterbringen?
Man könnte sich eine unendlich große konische Tüte vorstellen, die nach unten spitz zuläuft und die Tennisbällen enthält. Wenn man aber so eine Tüte von der Spitze aus von der Erde betrachtet, würde die Öffnung den ganzen Himmel ausfüllen. Die Öffnung wäre ja unendlich groß. Jetzt hat man aber ein Dilemma. Wenn mein "Sehstrahl"* flacher als die Tütenwand ist, wird er die Tüte nie treffen. So ergibt sich darum der Schluss, die Unendlichkeit ist nur ein Punkt**, von der Erde aus gesehen.
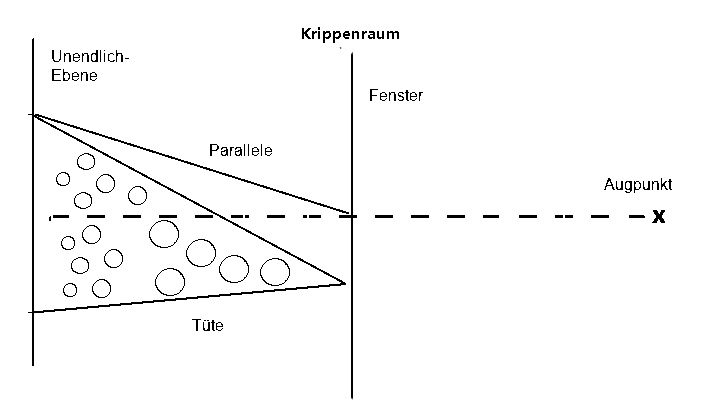
Der Sachverhalt sieht im Krippenraum anders aus. Im Krippenraum bildet die Tüte einen Horizontkreis auf der Unendlichkeitsebene. Der Krippenraum ist jedoch nur eine Abbildung des euklidischen Halbraums, nicht die physikalische Realität. In der Unendlichkeitsebene treffen sich alle Parallelen in einen Punkt.

Ein mathematisches euklidisches Modell:
In einem xy-Koordinatensystem sind im ersten Quatranten zwei Halbgeraden zum Ursprung gezeichnet. Betrachtet man sie wenn x gegen Unendlich geht, so wird ihr Abstand unendlich groß. Im Endlichen treffen sie sich nie. Beide Geraden enden aber im Punkt x=∞, y=∞. Es zeigt sich: Mathematik ist nicht unbedingt Physik.

* Für Dummies:Blickrichtung
**Eine Lösung bietet die "Sinc-Kugel".

Ludwig Resch