Ist die Schwerkraft im Schwerpunkt vereint?

Bei kleinen Massen auf der Erde scheint das so. Wie ist das aber im Allgemeinen?
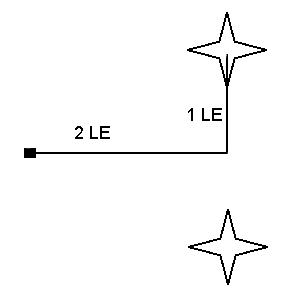
Eine kleine Masse X befindet sich nahe bei einem Doppelsternsystem. Die beiden Sterne sollen gleich groß sein. Ihr Abstand sei zwei Längeneinheiten (LE). Sie kreisen also in einer Bahn mit Radius LE um den Schwerpunkt S. Die Masse X soll im Abstand LE von einem Stern eine Schwerkraft 1 SE (Schwerkrafteinheit) bewirken. Die Masse X liegt fest in einer Entfernung von zwei LE vom Schwerpunkt der beiden Sterne. Im ersten Fall, wenn beide Sterne gleich weit von X stehen, ist der Abstand jeweils sqrt (5) LE nach Pytagoras . Die Kraft ist jeweils 1/ r² also 1/5 SE. Vom Kräfteparallelogramm ist die Resultierende 2 * 1/5 * cos (phi). phi ist der Winkel zur Mitte. cos (phi) ist daher 2/sqrt (5). Die gesamte Schwerkraft ergibt sich so zu (4 /25)* sqrt (5)=0,358 SE.

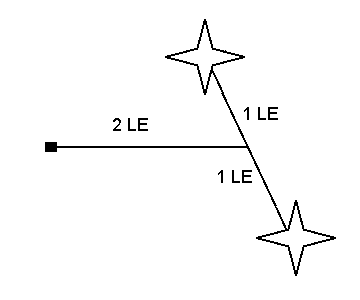Wenn sich die Sterne um 30° weiter drehen, bildet der nähere Stern ein rechtwinkliges Dreieck mit X und den Schwerpunkt S. Dieser Stern ist dann von X sqrt (3) LE entfernt, die Kraftkomponente von X zum Stern ist dann 1/3 SE.
Der andere Stern bildet zur Linie X S einen Winkel von 120°. Das Lot vom Stern auf die Verlängerung dieser Linie ergibt die Höhe eines gleichseitigen Dreiecks. Diese Höhe ist deshalb sqrt (3/4) LE groß. Der Fußpunkt ist zu X 2,5 LE entfernt. Deshalb beträgt der Abstand des zweiten Sternes zu X sqrt( 2,5 *2,5+3/4)=sqrt(7) LE, mit der Kraft 1/7 SE

Der Kraftvektor k2 hat dann die Koordinaten:
x2=1 /7 * cos(phi2) SE=5*sqrt(7)/98 SE. y2=-1/7 * sin(phi2) SE=-sqrt(3/7)/14 SE.

Die Summe beider Vektoren
xs = sqrt (3)/6 +5*sqrt(7)/98 SE=(sqrt(3)* 49+sqrt(7)*15)/294 SE=0.424 SE
ys = 1/6 -sqrt(3/7)/14 SE=7/42-3*sqrt(3/7)/42 SE=0.120 SE
Den Betrag der resultierenden Kraft erhält man aus
sr = sqrt(xs*xs+ys*ys)=0,440 SE. sin (phi res)=ys/sr=0,272. phi=arcsin(ain)*180/pi=15,8°
Der Kraftvektor zeigt hier also nicht mehr auf den Schwerpunkt.